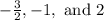Question

Given f(x)=2x^3+x^2-7x-6. Find all real and imaginary zeroes. Show your work.

Answer 1

The real zeroes of given function is
`-(3)/(2),-1, \text { and } 2`

Solution:

Given that,
`f(x)=2 x^(3)+x^(2)-7 x-6`

We have to find the real and imaginary zeroes

This can be found out by equating the function to zero and finding the roots "x"

Now, let us use trail and error method.

So put x = 1 in f(x)

f(1) = 2 + 1 – 7 – 6 = - 10

1 is not a root. Since f(1) is not equal to 0

Now put x = -1

f(-1) = -2 + 1 + 7 – 6 = 0

-1 is a root. Since f(-1) is equal to 0

So, one of the roots is -1. Let the other roots be a, b.

`\text { Sum of roots }=\frac{-x^(2) \text { coefficient }}{x^(3) \text { coefficient }}`

`\begin{array}{l}{a+b+(-1)=(-1)/(2)} \\\\ {a+b=1-(1)/(2)} \\\\ {a+b=(1)/(2) \rightarrow(1)}\end{array}`

`\begin{array}{l}{\text {Product of roots }=\frac{-\text {constant}}{x^(3) \text {coefficient}}} \\\\ {a b(-1)=(-(-6))/(2)} \\\\ {a b(-1)=3} \\\\ {a b=-3 \rightarrow(2)}\end{array}`

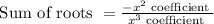
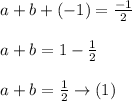
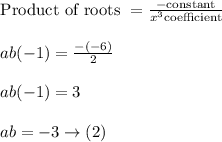
Now, we know that, algebraic identity,

`\begin{array}{l}{(a-b)^(2)=(a+b)^(2)-4 a b} \\\\ {(a-b)^2=\left((1)/(2)\right)^(2)-4(-3)} \\\\ {(a-b)^2=(1)/(4)+12} \\\\ {(a-b)^2=(49)/(4)} \\\\ {a-b=(7)/(2) \rightarrow(3)}\end{array}`

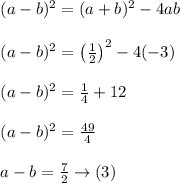
Add (1) and (3)

`\begin{array}{l}{2 a=(7+1)/(2) \rightarrow 2 a=4 \rightarrow a=2} \\\\ {\text { Then, from }(2) \rightarrow b=-(3)/(2)}\end{array}`

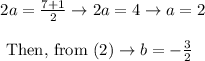
Hence, the roots of the given equation are
`-(3)/(2),-1, \text { and } 2`