Question

An elevator can safely hold 3,500 lbs. A sign in the elevator limits the passenger count to 15. If the adult population has a mean weight of 180 lbs with a 25 lbs standard deviation, how unusual would it be, if the central limit theorem applied, that an elevator holding 15 people would be carrying more than 3,500 pounds? (Hint: if X is a random variable indicating a person’s weight, then assume X Normal( = 180; 2 = 252); use related d, p, q, and r functions to get the numerical answer.)

Answer 1

`1.75*10^(-27)`

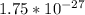
Explanation:

If, collectively, 15 people weigh more than 3500 pounds, that means each person must weigh more than 3500/15 = 233.33 pounds.

If the distribution for population weights is normal at mean = 180 and standard deviation = 25 lbs, that means the probability for 1 person to weigh higher than 233 lbs is

`1 - P(x > 233, \mu = 180, \sigma = 25) = 1 - 0.984 = 0.016`

For all 15 people to have higher weigh than that then the probability is

`0.016^(15) = 1.75*10^(-27)`

This is indeed very unlikely to happen