Answer:
a)
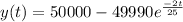
b)
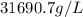
Explanation:
By definition, we have that the change rate of salt in the tank is
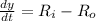 , where
, where
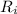 is the rate of salt entering and
is the rate of salt entering and
 is the rate of salt going outside.
is the rate of salt going outside.
Then we have,
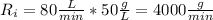 , and
, and
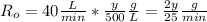
So we obtain.
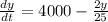 , then
, then
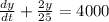 , and using the integrating factor
, and using the integrating factor
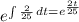 , therefore
, therefore
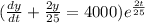 , we get
, we get
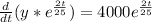 , after integrating both sides
, after integrating both sides
 , therefore
, therefore
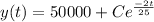 , to find
, to find
 we know that the tank initially contains a salt concentration of 10 g/L, that means the initial conditions
we know that the tank initially contains a salt concentration of 10 g/L, that means the initial conditions
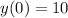 , so
, so

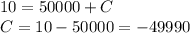
Finally we can write an expression for the amount of salt in the tank at any time t, it is
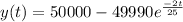
b) The tank will overflow due Rin>Rout, at a rate of
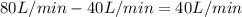 , due we have 500 L to overflow
, due we have 500 L to overflow
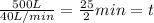 , so we can evualuate the expression of a)
, so we can evualuate the expression of a)
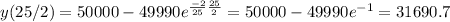 , is the salt concentration when the tank overflows
, is the salt concentration when the tank overflows