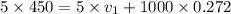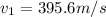Question

A 5.00-g bullet is shot through a 1.00-kg wood block suspended on a string 2.00 m long. The center of mass of the block rises a distance of 0.38 cm. Find the speed of the bullet as it emerges from the block if its initial speed is 450 m/s

Answer 1

Answer:395.6 m/s

Step-by-step explanation:

Given

mass of bullet
`m=5 gm`

mass of wood block
`M=1 kg`

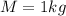
Length of string
`L=2 m`

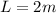
Center of mass rises to an height of
`0.38 cm`

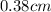
initial velocity of bullet
`u=450 m/s`

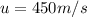
let
`v_1` and
`v_2` be the velocity of bullet and block after collision

Conserving momentum

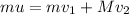`mu=mv_1+Mv_2` -------------1

Now after the collision block rises to an height of 0.38 cm

Conserving Energy for block

kinetic energy of block at bottom=Gain in Potential Energy

`(Mv_2^2)/(2)=Mgh_(cm)`

`v_2=\sqrt{2gh_(cm)}`

`v_2=√(2* 9.8* 0.38)`

`v_2=0.272 m/s`

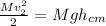
substitute the value of
`v_2` in equation 1

`5* 450=5* v_1+1000* 0.272`

`v_1=395.6 m/s`