Answer:
The distance h above the victim's arm where the level of the blood in the transfusion bottle should be located is 0.254 m
Step-by-step explanation:
given information:
density, ρ = 1060
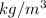
viscosity, η = 4 x
 Pa.s
Pa.s
needle length, L = 3 cm = 0.03 m
radius, r = 0.25 mm = 0.00025 m
volume flow rate, Q = 4.70 x

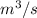
according to Poiseuille’s law
Q = (π
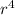 ΔP)/8ηL
ΔP)/8ηL
ΔP = (8QηL)/(π
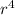 )
)
= 8 (4.70 x
 )(4 x
)(4 x
 )(0.03)/(π
)(0.03)/(π
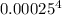 )
)
= 3676.71
Now we can calculate the distance h
ΔP = ρ g h
h = ΔP / ρ g
= 3676.71/(1060)(9.8)
= 0.354 m