Answer:
-$0.90
Explanation:
There are only two possible outcomes, winning $23 (W) or losing $15 (L). Therefore:
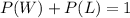
The probability of the player making his next 3 free throws (P(W)) is:
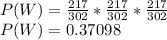
The probability of the player NOT making his next 3 free throws (P(L)) is:
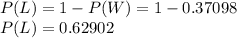
Expected value (EV) is given by the payoff of each outcome multiplied by its probability:
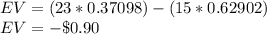
The expected value of the proposition is -$0.90