Question

A function y(t) satisfies the differential equation dy dt = y 4 − 6y 3 + 5y 2 . (a) What are the constant solutions of the equation? (Recall that these have the form y = C for some constant, C.) (b) For what values of y is y increasing? (c) For what values of y is y decreasing?

Answer 1

a) y = 0 , 5,1

b) y ⊂ (- ∞,0) ∪ (0,1)∪(5,∞)

Explanation:

Given data:

differential equation is given as

`\frac{dy}[dt} = y^4 -6y^3+ 5y^2`

a) constant solution

`y^4 -6y^3+ 5y^2 = 0`

taking y^2 from all part

`y^2(y^2 - 6y -5) = 0`

solution of above equation is

y = 0 , 5,1

b) for which value y is increasing

`(dy)/(dt)  > 0`

y^2(y - 5) (y -1) > 0

y ⊂ (- ∞,0) ∪ (0,1)∪(5,∞)

Answer 2

Hence increasing in (-\infty,0) U (1,5)

c) Decreasing in (0,1)

Explanation:

Given that y(t) satisfies the differential equation

`(dy)/(dt) =y^4-6y^2+5y^2\\=y^2(y^2-6y+5)\\=y^2(y-1)(y-5)`

Separate the variables to have

`(dy)/(y^2(y-1)(y-5)) =dt`

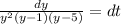
Left side we can resolve into partial fractions

Let
`(1)/(y^2(y-1)(y-5)) =(A)/(y) +(B)/(y^2)+(C)/(y-1) (D)/(y-5)`

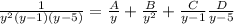
Taking LCD we get

`1= Ay(y-1)(Y-5) +B(y-1)(y-5)+Cy^2 (y-5)+Dy^2 (y-1)\\Put y =1\\1 =  -4C\\Put y =5\\ 1 = 25(4)D\\Put y =0\\1=5B\\`

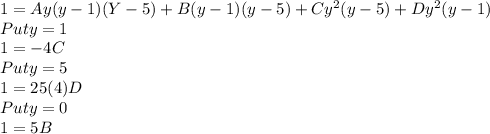
By equating coeff of y^3 we have

A+C+D=0

`C=(-1)/(4) \\D=(1)/(100) \\B =(1)/(5) \\A = -C-D = (6)/(25)`

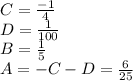
Hence left side =

`(6)/(25y) +(1)/(5y^2)+(-1)/(4(y-1))+ (1)/(100(y-5))=dt\\(6)/(25)ln y -(1)/(5y)-(1)/(4)ln|(y-1)| +(1)/(100)ln|y-5| = t+C`

b) y is increasing whenever dy/dt>0

dy/dt =0 at points y =0, 1 and 5

dy/dt >0 in (-\infty,0) U (1,5)

Hence increasing in (-\infty,0) U (1,5)

c) Decreasing in (0,1)