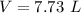Question

When you drink cold water, your body must expend metabolic energy in order to maintain normal body temperature (37° C) by warming up the water in your stomach. Could drinking ice water, then, substitute for exercise as a way to "burn calories?" Suppose you expend 286 kilocalories during a brisk hour-long walk. How many liters of ice water (0° C) would you have to drink in order to use up 286 kilocalories of metabolic energy? For comparison, the stomach can hold about 1 liter.

Answer 1

`V=7.73\ L`

Step-by-step explanation:

Given:

Initial temperature of water,
`T_i=0^(\circ)C`

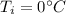
final temperature of water,
`T_f=37^(\circ)C`

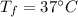
energy spent in one hour of walk,
`286\ kilocal=(286* 4186)\ J`

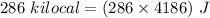
volumetric capacity of stomach,
`V=1\ L`

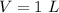
Now, let m be the mass of water at zero degree Celsius to be drank to spend 286 kilo-calories of energy.

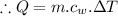`\therefore Q=m.c_w.\Delta T` .....................................(1)

where:

m = mass of water

Q = heat energy

`c_w=4186\ J\ (specific\ heat\ of\ water)`

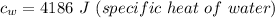
`\Delta T`= temperature difference

Putting values in the eq. (1):

`286* 4186=m* 4186* 37`

`m=7.73\ kg`

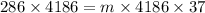
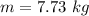
Since water has a density of 1 kilogram per liter, therefore the volume of water will be:

`V=7.73\ L`

Answer 2

7.72 Liters

Step-by-step explanation:

normal body temperature = T_body =37° C

temperature of ice water = T_ice =0°c

specfic heat of water = c_{water} =4186J/kg.°C

if the person drink 1 liter of cold water mass of water is = m = 1.0kg

heat lost by body is Qwater =mc_{water} ΔT

= mc{water} ( T_ice - T_body)

= 1.0×4186× (0 -37)

= -154.882 ×10^3 J

here negative sign indicates the energy lost by body in metabolic process energy expended due to brisk - hour long walk is Q_{walk} = 286 kilocalories

= 286×4186J

so number of liters of ice water have to drink is

n×Q_{water} =Q_{walk} n= Q_{walk}/ Q_{water}

= 286×4186J/154.882×10^3 J

= 7.72 Liters