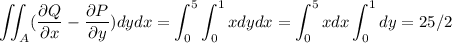Question

Evaluate the line integral by the two following methods. xy dx + x2 dy C is counterclockwise around the rectangle with vertices (0, 0), (5, 0), (5, 1), (0, 1) (a) directly -25 Incorrect: Your answer is incorrect. (b) using Green's Theorem 50 Incorrect: Your answer is incorrect.

Answer 1

25/2

Explanation:

Recall that for a parametrized differentiable curve C = (x(t), y(t)) with the parameter t varying on some interval [a, b]

`\large \displaystyle\int_(C)[P(x,y)dx+Q(x,y)dy]=\displaystyle\int_(a)^(b)[P(x(t),y(t))x'(t)+Q(x(t),y(t))y'(t)]dt`

Where P, Q are scalar functions

We want to compute

`\large \displaystyle\int_(C)P(x,y)dx+Q(x,y)dy=\displaystyle\int_(C)xydx+x^2dy`

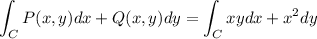
Where C is the rectangle with vertices (0, 0), (5, 0), (5, 1), (0, 1) going counterclockwise.

a) Directly

Let us break down C into 4 paths
`\large C_1,C_2,C_3,C_4` which represents the sides of the rectangle.

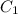`\large C_1` is the line segment from (0,0) to (5,0)

`\large C_2` is the line segment from (5,0) to (5,1)

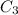`\large C_3` is the line segment from (5,1) to (0,1)

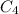`\large C_4` is the line segment from (0,1) to (0,0)

Then

`\large \displaystyle\int_(C)=\displaystyle\int_(C_1)+\displaystyle\int_(C_2)+\displaystyle\int_(C_3)+\displaystyle\int_(C_4)`

Given 2 points P, Q we can always parametrize the line segment from P to Q with

r(t) = tQ + (1-t)P for 0≤ t≤ 1

Let us compute the first integral. We parametrize
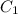`\large C_1` as

r(t) = t(5,0)+(1-t)(0,0) = (5t, 0) for 0≤ t≤ 1 and

r'(t) = (5,0) so

`\large \displaystyle\int_(C_1)xydx+x^2dy=0`

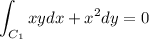
Now the second integral. We parametrize
`\large C_2` as

r(t) = t(5,1)+(1-t)(5,0) = (5 , t) for 0≤ t≤ 1 and

r'(t) = (0,1) so

`\large \displaystyle\int_(C_2)xydx+x^2dy=\displaystyle\int_(0)^(1)25dt=25`

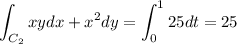
The third integral. We parametrize
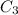`\large C_3` as

r(t) = t(0,1)+(1-t)(5,1) = (5-5t, 1) for 0≤ t≤ 1 and

r'(t) = (-5,0) so

`\large \displaystyle\int_(C_3)xydx+x^2dy=\displaystyle\int_(0)^(1)(5-5t)(-5)dt=-25\displaystyle\int_(0)^(1)dt+25\displaystyle\int_(0)^(1)tdt=\\\\=-25+25/2=-25/2`

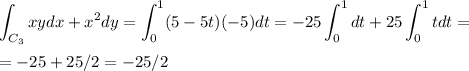
The fourth integral. We parametrize
`\large C_4` as

r(t) = t(0,0)+(1-t)(0,1) = (0, 1-t) for 0≤ t≤ 1 and

r'(t) = (0,-1) so

`\large \displaystyle\int_(C_4)xydx+x^2dy=0`

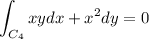
So

`\large \displaystyle\int_(C)xydx+x^2dy=25-25/2=25/2`

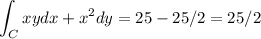
Now, let us compute the value using Green's theorem.

According with this theorem

`\large \displaystyle\int_(C)Pdx+Qdy=\displaystyle\iint_(A)(\displaystyle(\partial Q)/(\partial x)-\displaystyle(\partial P)/(\partial y))dydx`

where A is the interior of the rectangle.

so A=(x,y)

We have

`\large \displaystyle(\partial Q)/(\partial x)=2x\\\\\displaystyle(\partial P)/(\partial y)=x`

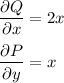
so

`\large \displaystyle\iint_(A)(\displaystyle(\partial Q)/(\partial x)-\displaystyle(\partial P)/(\partial y))dydx=\displaystyle\int_(0)^(5)\displaystyle\int_(0)^(1)xdydx=\displaystyle\int_(0)^(5)xdx\displaystyle\int_(0)^(1)dy=25/2`