Question

A disc of moment of inertia 1.8 k g.m2 is rotating at a constant angular velocity of 3.2 rad.s−1. A second disc of moment of inertia 0.6 kg.m2, initailly at rest, falls on the first disc and the two rotate as a system. What is the angular velocity of the system?

Answer 1

2.4 rad/s

Step-by-step explanation:

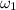`\omega_1` = Initial angular velocity = 3.2 rad/s

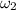`\omega_2` = Final angular velocity of the system

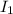`I_1` = Initial angular momentum = 1.8 kgm²

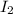`I_2` = Final angular momentum = 0.6 kgm²

As there is no external torque then the angular momentum in the system is conserved

`I_1\omega_1=(I_1+I_2)\omega_2\\\Rightarrow \omega_2=(I_1\omega_1)/(I_1+I_2)\\\Rightarrow \omega_2=(1.8* 3.2)/(1.8+0.6)\\\Rightarrow \omega_2=2.4\ rad/s`

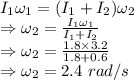
The angular velocity of the system is 2.4 rad/s