Question

A 9.08 m ladder with a mass of 23.8 kg lies flat on the ground. A painter grabs the top end of the ladder and pulls straight upward with a force of 260 N. At the instant the top of the ladder leaves the ground, the ladder experiences an angular acceleration of 1.78 rad/s2 about an axis passing through the bottom end of the ladder. The ladder's center of gravity lies halfway between the top and bottom ends. (a) What is the net torque acting on the ladder? (b) What is the ladder's moment of inertia?

Answer 1

1300.80988 Nm

730.79206 kgm²

Step-by-step explanation:

m = Mass of ladder = 23.8 kg

g = Acceleration due to gravity = 9.81 m/s²

L = Length of ladder = 9.08 m

F = Applied force = 260 N

`\alpha` = Angular acceleration = 1.78 rad/s²

I = Moment of inertia

Weight is given by

`W=mg\\\Rightarrow W=23.8* 9.81\\\Rightarrow W=233.478\ N`

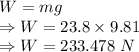
The center of gravity of the ladder lies at the center of the ladder

Torque will be

`\tau=-W* (L)/(2)+F* L\\\Rightarrow \tau=-233.478* (9.08)/(2)+260* 9.08\\\Rightarrow \tau=1300.80988\ Nm`

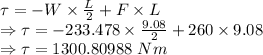
The net torque acting on the ladder is 1300.80988 Nm

Torque is also given by

`\tau=I\alpha\\\Rightarrow I=(\tau)/(\alpha)\\\Rightarrow I=(1300.80988)/(1.78)\\\Rightarrow I=730.79206\ kgm^2`

The moment of inertia of the ladder is 730.79206 kgm²