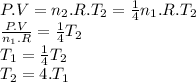Question

A chemist prepares a sample of helium gas at a certain pressure, temperature and volume and then removes all but a fourth of the gas molecules (only a fourth remain). How must the temperature be changed (as a multiple of T1) to keep the pressure and the volume the same?a. T2=1/16T1b. T2=2T1c. T2=16T1d. T2= 1/2T1e. T2=4T1f. None of theseg. T2=1/4T1

Answer 1

e. T₂= 4T₁

Step-by-step explanation:

Initially, we have a number of moles (n₁) a gas sample at a certain pressure (P), temperature (T₁) and volume (V). We can relate these variables through the ideal gas equation.

P . V = n₁ . R . T₁

where,

R is the ideal gas constant

We can rearrange this equation like:

`T_(1)=(P.V)/(n_(1).R)`

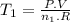
If only one fourth of the initial molecules remain n₂ = 1/4 n₁. The new temperature (T₂) assuming pressure and temperature remain constant is:

`P.V=n_(2).R.T_(2)=(1)/(4) n_(1).R.T_(2)\\(P.V)/(n_(1).R) =(1)/(4) T_(2)\\T_(1)=(1)/(4) T_(2)\\T_(2)=4.T_(1)`