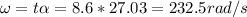Question

A 5.0-kg hollow cylinder of radius 0.37m rotates freely about an axle that runs through its center and along its long axis. A cord is wrapped around the cylinder and is pulled straight from the cylinder with a steady tensile force of 50 N . As the cord unwinds, the cylinder rotates, with no slippage between cord and cylinder.

A- Calculate the work done by the tensile force as the cylinder rotates through 1000 rad
B- If the cylinder starts from rest, calculate its rotational speed after it has rotated through 1000 rad .

Answer 1

A-18500J

B-232.5 rad/s

Step-by-step explanation:

A- As the cylinder rotates through 1000rad, it sweeps a distance of

`d = R\theta = 0.37*1000 = 370m`

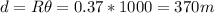
So the work, which is distance times force, of the tension done on the cylinder through that distance is

W = Td = 50 * 370 = 18500 J[/tex]

B- The torque that exerts on the cylinder by the tension is

To = TR = 50*0.37 = 18.5 Nm

As the cylinder is hollow, its moments of inertia is

`I = mR^2 = 5*0.37^2 = 0.6845  kgm^2`

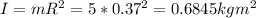
The torque is generating an angular acceleration of:

`\alpha = (To)/(I) = (18.5)/(0.6845) = 27.03rad/s^2`

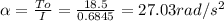
The time it takes to go from rest to 1000 rad

`t^2 = (2\theta)/(\alpha) = (2*1000)/(27.03) = 74`

`t = √(74) = 8.6s`

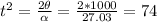
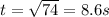
Therefore the final rotational speed is

`\omega = t\alpha =8.6*27.03 = 232.5 rad/s`