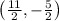2 Answers

Colin Steel · Answer 1 · 2020-02-03T09:22:06+0000

The midpoint of a line segment with endpoints at (3,-1) and (8, -4) is
$\left((11)/(2),-(5)/(2)\right)$

Solution:

We have been given 2 end points of a line which are: (3,-1) and (8, -4)

The midpoint of a line segment is half way from both the ends of the line segment.

The formula for midpoint for the two points
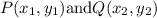$P(x_1, y_1) \text{and} Q(x_2, y_2)$ is given as:

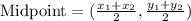
$\text {Midpoint}=((x_(1)+x_(2))/(2), (y_(1)+y_(2))/(2))$

Here P(3, -1) and Q(8, -4)

$\text { So } x_(1)=3 ; x_(2)=8 ; y_(1)=-1 ; y_(2)=-4$

Plugging in values in above formula, we get

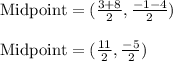
$\begin{array}{l}{\text {Midpoint}=((3+8)/(2), (-1-4)/(2)})\\\\ {\text {Midpoint}=((11)/(2), (-5)/(2)})\end{array}$

Hence, the midpoint of the line segment is
$\left((11)/(2),-(5)/(2)\right)$

Please log in or register to add a comment.