Answer:
Since p value <0.1 accept the claim that oven I repair costs are more
Explanation:
The data given for two types of ovens are summarised below:
Group Group One Group Two
Mean 85.7900 78.6700
SD 15.1300 17.8400
SEM 1.9533 2.3840
N 60 56
Alpha = 10%
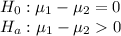
(Right tailed test)
The mean of Group One minus Group Two equals 7.1200
df = 114
standard error of difference = 3.065
t = 2.3234
p value = 0.0219
If p value <0.10 reject null hypothesis
4) Since p value <0.1 accept the claim that oven I repair costs are more