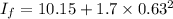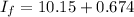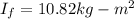Question

A potter's wheel has the shape of a solid uniform disk of mass 13.0 kg and radius 1.25 m. It spins about an axis perpendicular to the disk at its center. A small 1.7 kg lump of very dense clay is dropped onto the wheel at a distance 0.63 m from the axis. What is the moment of inertia of the system about the axis of spin?

Answer 1

Answer:
`10.82 kg-m^2`

Step-by-step explanation:

Given

Mass of solid uniform disk
`M=13 kg`

radius of disk
`r=1.25 m`

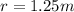
mass of lump
`m=1.7 kg`

distance of lump from axis
`r_0=0.63`

Moment of inertia is the distribution of mass from the axis of rotation

Initial moment of inertia of disk
`I_1=(Mr^2)/(2)`

`I_1=(13* 1.25^2)/(2)=10.15 kg-m^2`

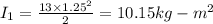
Final moment of inertia
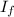`I_f`=Moment of inertia of disk+moment of inertia of lump about axis

`I_f=(Mr^2)/(2)+mr_0^2`

`I_f=10.15+1.7* 0.63^2`

`I_f=10.15+0.674`

`I_f=10.82 kg-m^2`