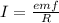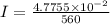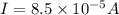Answer:
(a) E= 3.36×10−2 V +( 3.30×10−4 V/s3 )t3
(b)
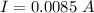
Step-by-step explanation:
Given:
- radius if the coil,
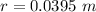
- no. of turns in the coil,
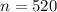
- variation of the magnetic field in the coil,

- resistor connected to the coil,
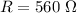
(a)
we know, according to Faraday's Law:

where:
 change in associated magnetic flux
change in associated magnetic flux
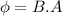
where:
A= area enclosed by the coil
Here
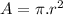
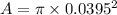


So, emf:
![emf= 520* (d)/(dt) [((1.2* 10^(-2))t+(3.45* 10^(-5))t^4)* 0.0049]](https://img.qammunity.org/2020/formulas/physics/college/7prao832r1cvems68zwx24yai6arny222e.png)
![emf= 520* 0.0049* (d)/(dt) [(1.2* 10^(-2))t+(3.45* 10^(-5))t^4)]](https://img.qammunity.org/2020/formulas/physics/college/pidkmlca2hugv0ngya9a66yldrqflgidux.png)
![emf= 2.548* [0.012+(13.8* 10^(-5))t^3)]](https://img.qammunity.org/2020/formulas/physics/college/omrqx4z00ajp283eopqbzok43x5554qgoo.png)

(b)
Given:
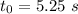
Now, emf at given time:
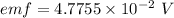
∴Current