Question

The heights of adult men in America are normally distributed, with a mean of 69.3 inches and a standard deviation of 2.64 inches. The heights of adult women in America are also normally distributed, but with a mean of 64.5 inches and a standard deviation of 2.53 inches. a) If a man is 6 feet 3 inches tall, what is his z-score (to two decimal places)? z = 2.16 b) What percentage of men are SHORTER than 6 feet 3 inches? Round to nearest tenth of a percent.

Answer 1

z-score is 2.16

98.46% of men are SHORTER than 6 feet 3 inches

Explanation:

The heights of adult men in America are normally distributed, with a mean of 69.3 inches and a standard deviation of 2.64 inches.

Mean =
`\mu = 69.3 inches`

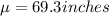
Standard deviation =
`\sigma = 2.64 inches`

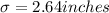
a) If a man is 6 feet 3 inches tall, what is his z-score (to two decimal places)

x = 6 feet 3 inches

1 feet =12 inches

6 feet = 12*6 = 72 inches

So, x = 6 feet 3 inches = 72+3=75 inches

Formula :
`Z=(x-\mu)/(\sigma)`

`Z=(75-69.3)/(2.64)`

`Z=2.159`

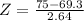
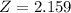
So, his z-score is 2.16

No to find percentage of men are SHORTER than 6 feet 3 inches

We are supposed to find P(x< 6 feet 3 inches)

z-score is 2.16

Refer the z table

P(x< 6 feet 3 inches) =0.9846

So, 98.46% of men are SHORTER than 6 feet 3 inches