Answer:
(a)
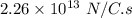
(b) 5 A
Solution:
As per the question:
Radius of the circular plate, R = 9 cm = 0.09 m
Distance, d = 2.0 mm =
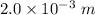
At
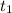 , current, I = 5 A
, current, I = 5 A
Now,
Area, A =
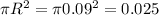
We know that the capacitance of the parallel plate capacitor, C =

Also,
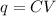
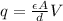
Also,
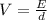
Now,
(a) The rate of change of electric field:
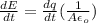
where
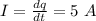
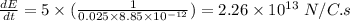
(b) To calculate the displacement current:

where
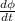 = Rate of change of flux
= Rate of change of flux

