Question

A soup can is in the shape of a right cylinder. The can has a volume of 16 fluid ounces. The height is three times its radius. The metal used to make the lateral surface of the can costs $0.01 per square inch. The metal used to make the top and bottom costs $0.02 per square inch. If one fluid ounce is approximately 1.805 cubic inches, what is the total cost to make one empty soup can? Use 3.14 for straight pi

Answer 1

$0.662772

Step-by-step explanation:

v = Volume of can = 16 fl oz.

`1\ floz.=1.805\ in^3`

r = Radius of can

h = Height of can = 3r

Volume of cylinder is given by

`\pi r^2h=16* 1.805\\\Rightarrow \pi r^23r=16* 1.805\\\Rightarrow 3\pi r^3=16* 1.805\\\Rightarrow r=\left((16* 1.805)/(3* 3.14)\right)^{(1)/(3)}\\\Rightarrow r=1.45247\ in`

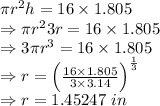
h=3r\\\Rightarrow h=3\times 1.45247\\\Rightarrow h=4.35741\ in[/tex]

Surface area of sides is given by

`2\pi rh\\ =2* 3.14* 1.45247* 4.35741\\ =39.76632\ in^2`

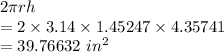
Surface area of top and bottom is given by

`2\pi r^2\\ =2* 3.14* 1.45247^2\\ =13.25544\ in^2`

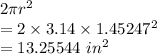
Cost of making the can will be

`39.76632* 0.01+13.25544* 0.02=\$0.662772`

The cost to make the can is $0.662772