Answer:
F = 3.2 x 10⁻¹⁹ x (6i - 3j + 5k) N
Step-by-step explanation:
Magnetic fields exert forces on moving charge. The force F exerted by a magnetic field B on a charge q moving with velocity v in an electric field is called the magnetic Lorentz force. It is given by
F = qv × B
The magnitude of the Lorentz force F is F = qvB sinθ, where θ is the smallest angle between the directions of the vectors v and magnetic field B. When v and B are perpendicular to each other, sinθ = 1 then F has its maximum possible magnitude F = qv x B
Given:
Instantaneous velocity v = vyj + vzk but vy =5m/s and vz =3m/s.
v = 5j + 3k m/s
Field B = Bxj + Byj but Bx =2T and By =4T
B = 2i + 4j T
From magnetic Lorentz force F = q v x B
F = −1.6 × 10⁻¹⁹ x [ (5j + 3k) X (2i + 4j) ]
solving vector multiplication of V X B
![V X B =\left[\begin{array}{ccc}i&-j&k\\0&5&3\\2&4&0\end{array}\right]](https://img.qammunity.org/2020/formulas/physics/college/ki0nigckme9dzfwzr2uxg9tyw57t9lqzch.png)
![=\left[\begin{array}{ccc}5&3\\4&0\\\end{array}\right] i - \left[\begin{array}{ccc}0&3\\2&0\\\end{array}\right] j + \left[\begin{array}{ccc}0&5\\2&4\\\end{array}\right] k](https://img.qammunity.org/2020/formulas/physics/college/4p1f8ohyjfuyes50rlgyywnyguutbm4itf.png)
=
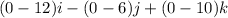
V X B =
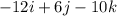
F = −1.6 × 10⁻¹⁹ x (-12i + 6j -10k)
Expanding the bracket and simplifying to the lowest term;
F = 3.2 x 10⁻¹⁹ x (6i - 3j + 5k) N