Question

A wheel with a weight of 395 N comes off a moving truck and rolls without slipping along a highway. At the bottom of a hill it is rotating at an angular velocity of 23.1 rad/s . The radius of the wheel is 0.652 m and its moment of inertia about its rotation axis is 0.800 MR2. Friction does work on the wheel as it rolls up the hill to a stop, at a height of h above the bottom of the hill; this work has a magnitude of 3470 J .

Answer 1

h=12.04m

Step-by-step explanation:

1) Notation and some important concepts

`\omega_i` represent the initial angular velocity

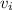`v_i` represent the initial velocity

`h` represent the final height reached by the mass

`M` represent the mass of the object

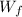`W_f` represent the work due the friction force (variable of interest)

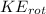`KE_(rot)` represent the rotational energy

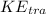`KE_(tra)` represent the transitional kinetic energy

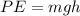`PE=mgh` represent the potential energy

`I=0.8MR^2` represent the rotational inertia

W= 395 N is the weight of the object

For this problem we can use the principle of energy conservation, this principle states that "the total energy of an isolated system remains constant; it is said to be conserved over time".

At the begin the wheel had rotational energy defined as "The kinetic energy due to rotational motion. Is a scalar quantity and have units of energy usually Joules". And this energy is represented by the following formula:
`KE_(rot)=(1)/(2)I\omega^2_i`

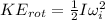
At the starting point the wheel also had kinetic energy defined as "The energy of mass in motion" and is given by the formula :
`KE_(tran)=(1)/(2)mv_i^2_i`

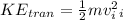
At the end of the movement we have potential energy since the mass is at height h the potential energy is defined as "The energy stored within an object, due to the object's position, arrangement or state" and is given by the formula
`PE=mgh`.

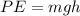Since we have friction acting we have a work related to the force of friction and we need to subtract this from the formula of conservation of energy

2) Formulas to use

The figure attached is an schematic draw for the problem

Using the principle of energy conservation we have:

`KE_(rot)+KE_(tran)-W_f =PE`

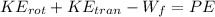
Replacing the formulas for each energy w ehave:

`(1)/(2)I\omega^2_i+(1)/(2)mv_i^2_i-W_f =Mgh` (1)

We also know that
`v_i =\omega_i R` and
`I=0.8MR^2` so if we replace this into equation (1) we got:

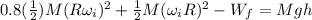`0.8((1)/(2))M(R\omega_i)^2 +(1)/(2)M(\omega_i R)^2-W_f=Mgh` (2)

We also know that the weight is defined as
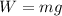`W=mg` so then
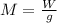`M=(W)/(g)`, so if we replace this into equation (2) we have:

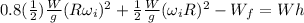`0.8((1)/(2))(W)/(g)(R\omega_i)^2 +(1)/(2)(W)/(g)(\omega_i R)^2-W_f=Wh` (3)

So then if we solve for h we got:

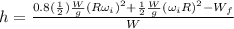`h=(0.8((1)/(2))(W)/(g)(R\omega_i)^2 +(1)/(2)(W)/(g)(\omega_i R)^2-W_f)/(W)` (4)

3) Solution for the problem

Now we can replace the values given into equation (4):

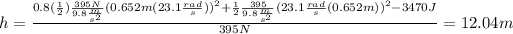`h=(0.8((1)/(2))(395N)/(9.8(m)/(s^2))(0.652m(23.1(rad)/(s)))^2 +(1)/(2)(395)/(9.8(m)/(s^2))(23.1(rad)/(s)(0.652m))^2-3470J)/(395N)=12.04m` (4)

So then our final answer would be h=12.04m