Question

A particle is in uniform circular motion about the origin of an xy coordinate system, moving clockwise with a period of 8.38 s. At one instant, its position vector is r-> = (1.27 i - 4.10 j ) m. At that instant, what is the x- component of the velocity (in m/s)?

Answer 1

x- component of the velocity = -3.56 i m/s

Step-by-step explanation:

Given that

Time period T= 8.38 s

Angular speed of the particle = ω

Time period T

`T=(2\pi)/(\omega)`

`8.38=(2\pi)/(\omega)`

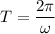
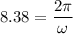
ω = 0.749 rad/s

Position vector given as

r= 1.27 i - 4.1 j

tanθ= 4.1 /1.27

θ = 72.74°

`r= √(1.27^2+4.1^2)\ m`

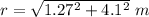
r= 4.92 m

The tangential velocity v

v= ω .r

v= 0.759 x 4.92 m/s

v=3.73 m/s

So the x component of velocity v = v cos(90° - 72.74°)

= 3.73 sin 72.74°

=3.56 m/s

The x- component of the velocity will in negative x direction.

So x- component of the velocity = - 3.56 i m/s