Answer:
Since, logarithm properties are,
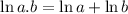
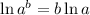
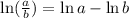
Given,
ln(2) ≈ 0.6931 and ln(3) ≈ 1.0986,
(a) ln(0.75) = ln(3/4)
= ln(3) - ln(4)
= ln(3) - ln(2²)
= ln(3) - 2ln (2)
= 1.0986 - 2(0.6931)
= -0.2876,
(b) ln(24) = ln(6 × 4)
= ln (6) + ln (4)
= ln (3 × 2) + ln(2²)
= ln (3) + ln(2) + 2 ln(2)
= ln 3 + 3 ln 2
= 1.0986 + 3(0.6931)
= 3.1779,
(c) ln (∛ 18)
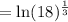
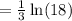
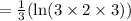
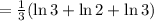
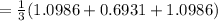
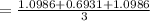
≈ 0.9634
(d)
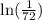

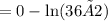
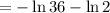
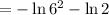
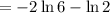
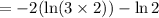
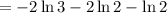
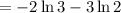
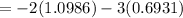
= -4.2765