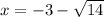Answer:
13.
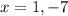
14.
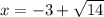 and
and
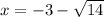
Explanation:
to solve the quadratic equation(
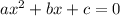 ) using completing the squares method:
) using completing the squares method:
Step1: divide the equation by a to make it in the form
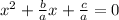
Step2: add
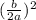 on both sides of the equation to get the eqaution:
on both sides of the equation to get the eqaution:
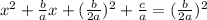
Step3: rearrange them to get the square.
⇒
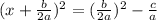
⇒
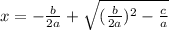 and
and
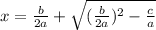
Now getting on to the question:
13.
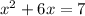
a=1; b=6; c=-7
adding
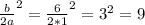 on both sides
on both sides
⇒

⇒
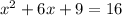
⇒
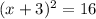
⇒
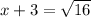
⇒
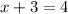 and
and
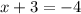
⇒
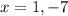
14.
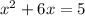
a=1; b=6; c=-5
adding
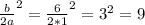 on both sides
on both sides
⇒
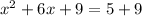
⇒
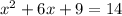
⇒
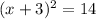
⇒
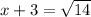
⇒
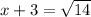 and
and
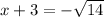
⇒
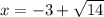 and
and