Question

A plane travels speed at 225 mph in still air. Flying with tailwind, the plane is clocked over distance of 875 miles. Flying against headwind, it takes 1 hour longer to complete the return trip. What is the wind velocity?

Answer 1

The wind speed is 28.466 mi/h

Explanation:

Let's call Vs=225mi/h the plane speed in still air. Let's have X=875 mi the distance traveled

We'll also call Vw the wind speed. In the first flight, the plane goes with a speed of Vs+Vw.

The return trip is made flying against a headwind with a speed of Vs-Vw

The time taken to travel X miles with a tailwind is

`t_1=(X)/(Vs+Vw)`

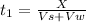
The time taken to travel X miles with a headwind is

`t_2=(X)/(Vs-Vw)`

We know
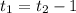`t_1=t_2-1` because the return trip is 1 hour longer. Then we have

`(X)/(Vs+Vw)=(X)/(Vs-Vw)-1`

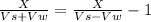
Multiplying by (Vs+Vw)(Vs-Vw)

`X(Vs-Vw)=X(Vs+Vw)-(Vs^2-Vw^2)`

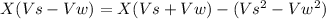
Replacing the values of X=875 and Vs=225 we reach a second-degree equation

`Vw^2+1750Vw-50625=0`

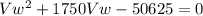
Which has the following roots:

Vw=28.466, Vw=-1778.466

We take the positive root and conclude

The wind speed is 28.466 mi/h

Note: We can easily check that the first time is 3.45h and the second time is 4.45h.