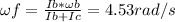Answer:
ωf = 4.53 rad/s
Step-by-step explanation:
By conservation of the angular momentum:
Ib*ωb = (Ib + Ic)*ωf
Where
Ib is the inertia of the ball
ωb is the initial angular velocity of the ball
Ic is the inertia of the catcher
ωf is the final angular velocity of the system
We need to calculate first Ib, Ic, ωb:
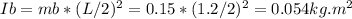
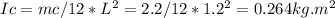
ωb = Vb / (L/2) = 16 / (1.2/2) = 26.67 m/s
Now, ωf will be: