Answer:
a) d(x)=

b)d'(x)=
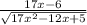
c)The critical point is x=
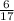
d)Closest point is (
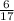 ,
,
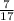
Explanation:
We are given the line
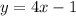
Let a point Q(
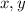 ) lie on the line.
) lie on the line.
Point P is given as P(2,0)
By distance formula, we have the distance D between any two points
A(
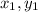 ) and B(
) and B(
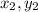 ) as
) as
D=
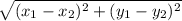
Thus,
d(x)=
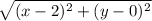
But we have,
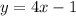
So,
d(x)=
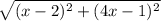
Expanding,
d(x)=
 - - - (a)
- - - (a)
Now,
d'(x)=
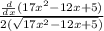
i.e.
d'(x)=
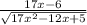 - - - (b)
- - - (b)
Now, the critical point is where d'(x)=0
⇒
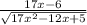 =0
=0
⇒
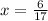 - - - (c)
- - - (c)
Now,
The closest point on the given line to point P is the one for which d(x) is minimum i.e. d'(x)=0
⇒
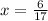
as
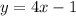
⇒y=
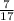
So, closest point is (
 ) - - -(d)
) - - -(d)