Question

Please find the answer and explain how you got it

Answer 1

m∠NQP=74°

Explanation:

we know that

The measure of the interior angles in a triangle must be equal to 180 degrees

In this problem

In the triangle NPQ

m∠N+m∠P+m∠Q=180°

we have

m∠N=(2x)°

m∠P=(34)°

m∠Q=(2x+2)°

substitute the values

`(2x)\°+(34)\°+(2x+2)\°=180\°`

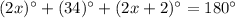
solve for x

`(4x+36)\°=180\°`

`4x=180-36`

`4x=144`

`x=36`

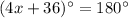
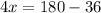
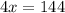
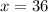
Find the measure of angle NQP

we know that

m∠NQP=m∠Q=(2x+2)°

substitute the value of x

m∠NQP=(2(36)+2)=74°