Answer:
The length of the sides are 9 units, 18 units and 11 units
Explanation:
Let
x ----> one side of the triangle
y ----> the longest side of the triangle
z ----> the third side of the triangle
we know that
The perimeter of triangle is equal to
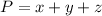
we have
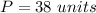
so
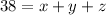 ----> equation A
----> equation A
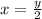 -----> equation B
-----> equation B
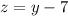 ----> equation C
----> equation C
substitute equation B and equation C in equation A
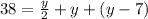
solve for y



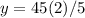
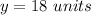
Find the value of x
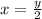 --->
--->
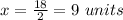
Find the value of z
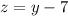 ---->
---->
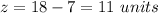
therefore
The length of the sides are 9 units, 18 units and 11 units