Question

How would I solve this?

Answer 1

The valid value of x is x=-2

Explanation:

we know that

The sum of the interior angles of any quadrilateral must be equal to 360 degrees

so

`(7x^(2)-24x)+100+(24-46x)+(3x^(2)+56)=360`

solve for x

Combine like terms

`10x^(2)-70x+180=360`

`10x^(2)-70x-180=0`

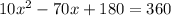
Divide by 10 both sides

`x^(2)-7x-18=0`

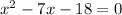
The formula to solve a quadratic equation of the form

`ax^(2) +bx+c=0`

is equal to

`x=\frac{-b(+/-)\sqrt{b^(2)-4ac}} {2a}`

in this problem we have

`x^(2)-7x-18=0`

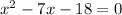
so

`a=1\\b=-7\\c=-18`

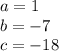
substitute in the formula

`x=\frac{-(-7)(+/-)\sqrt{-7^(2)-4(1)(-18)}} {2(1)}`

`x=\frac{7(+/-)√(121)} {2}`

`x=\frac{7(+/-)11} {2}`

`x=\frac{7(+)11} {2}=9`

`x=\frac{7(-)11} {2}=-2`

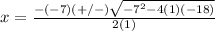
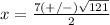
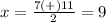
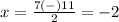
Remember that

The measure of the interior angle cannot be a negative number

For x=9

we have that the measure of one interior angle of quadrilateral is

`24-46x`

substitute the value of x

`24-46(9)=-390\°`

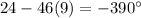
therefore

The value of x=9 cannot be a solution

For x=-2

The measure of the interior angles are

`(7(-2)^(2)-24(-2))=76\°\\100\°\\(3(-2)^(2)+56)=68\°\\24-46(-2)=116\°`

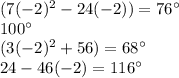
therefore

The valid value of x is x=-2