Question

Find the exact volume of a cone 6yd height 5yd base

Answer 1

The exact volume of a cone is 10 yd³.

Explanation:

Given:

Height of cone (h) is 6 yd and base (b) is 5 yd.

Now, to get the volume we need to find the radius.

So, to find radius we put the formula of base:

Let the radius be
`r`

Base=
`\pi r^2`

`b=\pi* r^(2)`

`5=\pi* r^(2)`

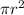
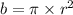
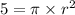
Dividing both sides by π and using square root on both the sides:

`5/ \pi=(\pi * r^(2)) / \pi`

`(5)/(\pi)=r^(2)`

`(5)/(\pi)=r^(2)`

`r^(2)=(5)/(\pi)-----1`

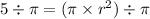
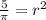
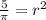
Now, putting the formula for getting the volume (v) of cone:

Volume =
`\pi r^2(h)/(3)`

`v=\pi* r^(2)* (6)/(3)`

`v=\pi* r^(2)* 2`

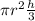
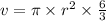
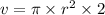
Substituting the value of
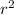`r^2` from equation (1), we get:

`v=\pi* (5)/(\pi)* 2`

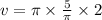
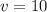`v=10` yd³

Volume of cone is 10 yd³

Therefore, the exact volume of a cone is 10 yd³.