Question

Find the x-coordinates of all critical points of the given function. Determine whether each critical point is a relative maximum, minimum, or neither by first applying the second derivative test, and, if the test fails, by some other method. f(x) = 5x4 − 2x3

Answer 1

f''(0.3) > 0 therefore,

x = 0.3 is point of minima

and,

f''(0) = 0

thus,

x = 0 is point of neither maxima nor minima

Explanation:

Given function:

f(x) = 5x⁴ − 2x³

Now,

To find the points of maxima or minima, put f'(x) = 0

thus,

f'(x) = (4)5x³ - (3)2x² = 0

or

20x³ - 6x² = 0

or

x(20x² - 6x) = 0

or

x = 0 and 20x² - 6x = 0

or

x = 0 and 2x(10x - 3) = 0

or

x = 0 and 2x = 0 and (10x - 3) = 0

or

x = 0 and x = 0 and x =
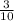`(3)/(10)` = 0.3

thus,

condition for maxima or minima

f''(x) = (3 × 4)5x² - (2 × 3)2x

or

f''(x) = 60x² - 12x

at

x = 0

f''(0) = 60(0)² - 12(0) = 0

at x = 0.3

f''(0.3) = 60(0.3)² - 12(0.3)

= 5.4 - 3.6

= 1.8

since,

f''(0.3) > 0 therefore,

x = 0.3 is point of minima

and,

f''(0) = 0

thus,

x = 0 is point of neither maxima nor minima