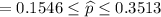Question

A trucking firm has a large inventory of spare parts that have been in storage for a long time. It knowsthat some proportion of these spare parts will have deteriorated to the point where they are no longerusable. In order to estimate this proportion, the firm tests 75 parts, and finds that 0.25 of them are notusable. Find the 95% confidence interval for the population proportion of parts that are not usable.

a. 0.25(1 0.25) 0.25(1 0.25) C 0.25 1.96 p 0.25 1.96 0.95 75 75
b. 0.25(1 0.25) 0.25(1 0.25) C 0.25 1.96 p 0.25 1.96 0.95 75 75
c. 0.25(1 0.25) 0.25(1 0.25) C 0.25 1.645 p 0.25 1.645 0.95 75 75
d. 0.25(1 0.25) 0.25(1 0.25) C 0.25 1.645 p 0.25 1.645 0.95 75 75

Answer 1

`0.1546\leq \widehat{p}\leq 0.3513`

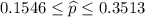
Explanation:

The firm tests 75 parts, and finds that 0.25 of them are notusable

n = 75

x = 0.25 \times 75 = 18.75≈19

`\widehat{p}=(x)/(n)`

`\widehat{p}=(19)/(75)`

`\widehat{p}=0.253`

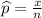
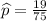
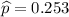
Confidence level = 95%

So, Z_\alpha at 95% = 1.96

Formula of confidence interval of one sample proportion:

`=\widehat{p}-Z_\alpha \sqrt{\frac{\widehat{p}(1-\widehat{p}}{n}}\leq \widehat{p}\leq \widehat{p}+Z_\alpha \sqrt{\frac{\widehat{p}(1-\widehat{p}}{n}}`

`=0.253-(1.96)\sqrt{(0.253(1-0.253))/(75)}\leq \widehat{p}\leq0.253+(1.96)\sqrt{(0.253(1-0.253)/(75)}`

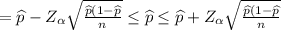
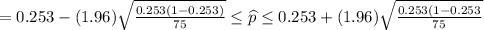
Confidence interval
`=0.1546\leq \widehat{p}\leq 0.3513`