Question

Two concentric spheres have radi of 5" and 6". Find the volume of the space between them.

Answer 1

The volume of the space between the two concentric spheres is 364π/3 cubic inches.

Explanation:

Given : Two concentric spheres have radii of 5" and 6".

So, to get the volume of the space between them.

Now, first we find the volume of both concentric spheres and after that we subtract smaller sphere volume from bigger sphere volume.

Putting the formula for getting the volume:

Volume of sphere(v) = 4/3πr³

So, for volume of sphere with radius 5":

Volume of sphere(v) =
`(4)/(3) \pi r^(3)`

`v=(4)/(3) \pi 5^(3)`

`v=(4)/(3)* \pi * 125`

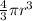
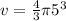
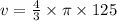
On solving, Volume of sphere(v) =
`(500)/(3) \pi cubic inches`.

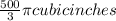Now, for sphere with radius 6":

Volume of sphere(V) =
`(4)/(3) \pi r^(3)`

`V=(4)/(3) \pi 6^(3)`

`v=(4)/(3)* \pi * 216`

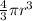
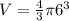
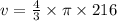
On solving, Volume of sphere(V) =
`(864)/(3) \pi cubic inches`.

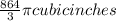So, the volume of the space between them = Volume of sphere with radius 6 - volume of sphere with radius 5:

`(864\pi )/(3) -(500\pi )/(3)`

`=\ (364\pi )/(3)`.

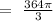Therefore, the volume of the space between the two concentric spheres is 364π/3 cubic inches.