Question

A box contains 3 coins. One coin has 2 heads and the other two are fair. A coin is chosen at random from the box and flipped. If the coin turns up heads, what is the probability that it is the two-headed coin? Is the answer 1/3? Was the answer intuitive?

Answer 1

Answer: Our required probability is
`(1)/(2)`

Explanation:

Since we have given that

Number of coins = 3

Number of coin has 2 heads = 1

Number of fair coins = 2

Probability of getting one of the coin among 3 =
`(1)/(3)`

So, Probability of getting head from fair coin =
`(1)/(2)`

Probability of getting head from baised coin = 1

Using "Bayes theorem" we will find the probability that it is the two headed coin is given by

`((1)/(3)* 1)/((1)/(3)* (1)/(2)+(1)/(3)* (1)/(2)+(1)/(3)* 1)\\\\=((1)/(3))/((1)/(6)+(1)/(6)+(1)/(3))\\\\=((1)/(3))/((2)/(3))\\\\=(1)/(2)`

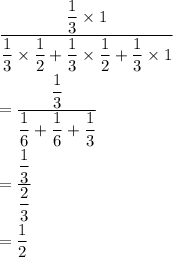
Hence, our required probability is
`(1)/(2)`

No, the answer is not
`(1)/(3)`