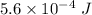Question

An empty capacitor is capable of storing 1.0 × 10-4 J of energy when connected to a certain battery. If the distance between the plates is halved and then filled with a dielectric (κ = 2.8), how much energy could this modified capacitor store when connected to the same battery?

Answer 1

`5.6* 10^(-4)\ J`

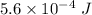
Step-by-step explanation:

d = Distance between capacitors

V = Voltage

k = Dielectric

A = Area

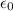`\epsilon_0` = Permittivity of free space

Energy the capacitor stores

`E=(1)/(2)CV^2=1* 10^(-4)\ J`

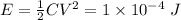
Capacitance is given by

`C=(k\epsilon_0A)/(d)\\\Rightarrow C=(\epsilon_0A)/(d)`

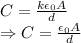
The new capacitance will be

`C'=(k\epsilon_0A)/((d)/(2))\\\Rightarrow C'=(2.8\epsilon_0A)/((d)/(2))\\\Rightarrow C'=(2.8\epsilon_0A* 2)/(d)\\\Rightarrow C'=(5.6\epsilon_0A)/(d)\\\Rightarrow C'=5.6C`

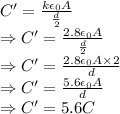
New energy will be

`E'=(1)/(2)CV^2\\\Rightarrow E'=(1)/(2)5.6CV^2\\\Rightarrow E'=5.6(1)/(2)CV^2\\\Rightarrow E'=5.6E\\\Rightarrow E'=5.6* 1* 10^(-4)\\\Rightarrow E'=5.6* 10^(-4)\ J`

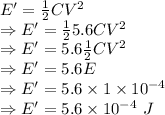
The energy the modified capacitor store when connected to the same battery is
`5.6* 10^(-4)\ J`