Answer: a) 0.079589 b) 0.079656
Explanation:
Since we have given that
Number of times a coin is flipped = 100 times
Number of times he get exactly head = 50
Probability of getting head =

We will use "Binomial distribution":
Probability would be

Using "Normal approximation":
n = 100
p = 0.5
So, mean =
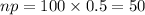
Standard deviation is given by
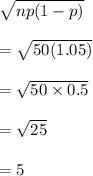
So,
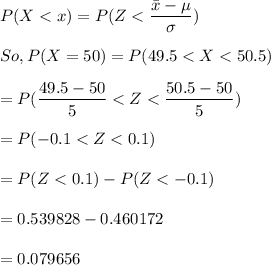
Hence, a) 0.079589 b) 0.079656