Answer:
The dimensions of the garden that minimize the cost is 9.018 feet(length) and 13.528 feet(width)
Explanation:
Let the length of garden be x
Let the breadth of garden be y
Area of Rectangular garden =
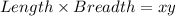
We are given that the area of the garden is 122 square feet
So,
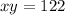 ---A
---A
A landscape architect wished to enclose a rectangular garden on one side by a brick wall costing $20/ft
So, cost of brick along length x = 20 x
On the other three sides by a metal fence costing $10/ft.
So, Other three side s = x+2y
So, cost of brick along the other three sides= 10(x+2y)
So, Total cost = 20x+10(x+2y)=20x+10x+20y=30x+20y
Total cost = 30x+20y
Substitute the value of y from A
Total cost =

Total cost =

Now take the derivative to minimize the cost
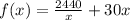
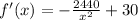
Equate it equal to 0
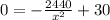
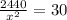
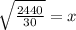
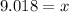
Now check whether it is minimum or not
take second derivative
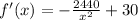
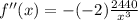
Substitute the value of x
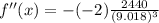
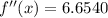
Since it is positive ,So the x is minimum
Now find y
Substitute the value of x in A
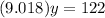


Hence the dimensions of the garden that minimize the cost is 9.018 feet(length) and 13.528 feet(width)