Question

A playground merry-go-round has radius 2.80 m and moment of inertia 2400 kg⋅m2 about a vertical axle through its center, and it turns with negligible friction.A child applies an 20.0 N force tangentially to the edge of the merry-go-round for 25.0 s . If the merry-go-round is initially at rest, what is its angular speed after this 25.0 s interval?

Answer 1

`\omega_f = 0.602\ rad/s`

Step-by-step explanation:

given,

radius of merry- go- round = 2.80 m

moment of inertia = I = 2400 kg⋅m²

child apply force tangentially = 20 N

for time = 25 s

angular speed after 25 speed = ?

initial angular speed of the merry go round = 0 rad/s

we know,

torque = I α.............(1)

α is angular acceleration

and also

τ = F.r........................(2)

computing equation (1) and (2)

F . r = I α

`\alpha = (\omega_f - \omega_i)/(t)`

`F . r =I * (\omega_f - \omega_i)/(t)`

`20 * 2.89 =2400* (\omega_f -0)/(25)`

`\omega_f = 0.602\ rad/s`

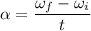
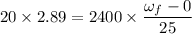
the angular speed of merry-go-round after 25 second is equal to
`\omega_f = 0.602\ rad/s`