Answer:
A manufacturer of banana chips would like to know whether its bag filling machine works correctly at the 447 gram setting.
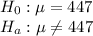
Mean =

n = 19
Since n < 30 , so we will use t test
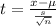
Substitute the values :
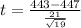
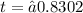
t calculated = -0.830
degree of freedom = n-1 = 19-1 = 18
A level of significance=α=0.025
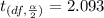
t critical = 2.093
t calculated < t critical
So, We failed to reject null hypothesis
Decision rule -0.830< 2.093 So, We failed to reject null hypothesis