Question

Suppose that a magnet high school includes grades 11 and 12, with half of the students in each grade. 60% of the senior class and 10% of the junior class are taking calculus. Suppose a calculus student is randomly selected to accompany the math teachers to a conference. What is the probability that the student is a junior? (Enter your answer as a fraction.)

Answer 1

Answer: Our required probability is
`(1)/(7)`

Explanation:

Since we have given that

P(Junior ) =
`(1)/(2)`

P(Senior) =
`(1)/(2)`

Let the given event be 'C' taking calculus.

P(C|J) = 10% = 0.10

P(C|S) = 60% = 0.60

We need to find the probability that the student is a junior.

So, our required probability is given by

`P(J|C)=(P(J).P(C|J))/(P(S).P(C|S)+P(J).P(C|J))\\\\P(J|C)=(0.5* 0.1)/(0.5* 0.1+0.5* 0.6)\\\\P(J|C)=(0.05)/(0.05+0.3)\\\\P(J|C)=(0.05)/(0.35)\\\\P(J|C)=(5)/(35)\\\\P(J|C)=(1)/(7)`

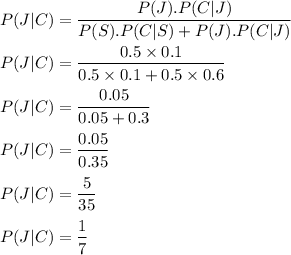
Hence, our required probability is
`(1)/(7)`