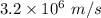Question

A vacuum-filled parallel plate capacitor has an energy density of 0.1 J/m^3 and the plates are separated by 0.2 mm.

An electron is released from rest near negativity charge plate of the capacitor.

How fast is the electron moving when it reaches the positively charged plate?

Answer 1

The speed of electron is
`3.2*10^(6)\ m/s`

Step-by-step explanation:

Given that,

Energy density = 0.1 J/m³

Separation = 0.2 mm

We need to calculate the potential difference

Using formula of energy density

`J=(1)/(2)\epsilon_(0)E^2`

`J=(1)/(2)\epsilon_(0)(V^2)/(d^2)`

`V^2=(0.1*(0.2*10^(-3))^2*2)/(8.85*10^(-12))`

`V^2=√(903.95)`

`V=30.06\ V`

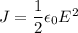
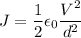
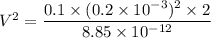
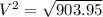
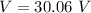
We need to calculate the speed of electron

Using energy conservation

`U=eV=(1)/(2)mv^2`

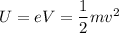
Put the value into the formula

`1.6*10^(-19)*30.06=(1)/(2)*9.1*10^(-31)* v^2`

`v^2=(1.6*10^(-19)*30.06*2)/(9.1*10^(-31))`

`v=\sqrt{1.057*10^(13)}`

`v=3.2*10^(6)\ m/s`

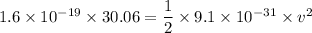
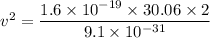
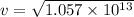
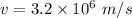
Hence, The speed of electron is
`3.2*10^(6)\ m/s`