Question

In a recent survey of drinking laws, a random sample of 1000 women showed that 65% were in favor of increasing the legal drinking age. In a random sample of 1000 men, 60% favored increasing the legal drinking age. Test the hypothesis that the percentage of men and women favoring a higher legal drinking age is the same. Use α = 0.05.

Answer 1

The percentage of men and women favoring a higher legal drinking age is the same

Explanation:

A random sample of 1000 women showed that 65% were in favor of increasing the legal drinking age

n = 1000

No. of females were in favor of increasing the legal drinking age =
`(65)/(100) * 1000=650`

y=650

In a random sample of 1000 men, 60% favored increasing the legal drinking age

n = 1000

No. of males were in favor of increasing the legal drinking age =
`(60)/(100) * 1000=600`

y=600

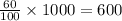
`n_1=1000 , y_1=650\\n_2=1000 , y_2=600`

We will use Comparing Two Proportions

`\widehat{p_1}=(y_1)/(n_1)`

`\widehat{p_1}=(650)/(1000)`

`\widehat{p_1}=0.65`

`\widehat{p_2}=(y_2)/(n_2)`

`\widehat{p_2}=(600)/(1000)`

`\widehat{p_2}=0.6`

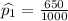
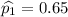
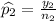
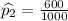
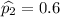
Let p_1 and p_2 be the probabilities of men and women favoring a higher legal drinking age is the same.

So,
`H_0:p_1=p_2\\H_a:p_1 \\eq p_2`

`\widehat{p}=(y_1+y_2)/(n_1+n_2) =(600+650)/(1000+1000)=0.625`

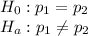
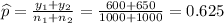
Formula of test statistic :
`\frac{\widehat{p_1}-\widehat{p_2}}{\sqrt{\widehat{p}(1-\widehat{p})((1)/(n_1)+(1)/(n_2))}}`

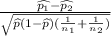
test statistic :
`\frac{0.65-0.6}{\sqrt{0.625(1-0.625)((1)/(1000)+(1)/(1000))}}`

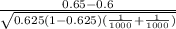
test statistic : 2.3094

Refer the z table for p value :

p value : 0.9893

α = 0.05.

p value > α

So, we failed to reject null hypothesis .

So, the percentage of men and women favoring a higher legal drinking age is the same