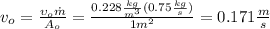Answer:
Inlet :
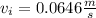
Outlet:
Step-by-step explanation:
1) Notation and important concepts
Flow of mass represent "the mass of a substance which passes per unit of time".
Flow rate represent "a measure of the volume of liquid that moves in a certain amount of time"
Specific volume is "the ratio of the substance's volume to its mass. It is the reciprocal of density."
Isentropic process is a "thermodynamic process, in which the entropy of the fluid or gas remains constant".
We know that the flow of mass is given by the following expression
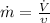 , where
, where
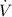 represent the flow rate and
represent the flow rate and
 the specific volume at the pressure and temperature given.
the specific volume at the pressure and temperature given.
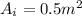 is the inlet area
is the inlet area
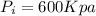 pressure at the inlet area
pressure at the inlet area
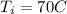 temperature at the inlet area
temperature at the inlet area
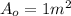 is the outlet area
is the outlet area
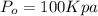 pressure at the outlet area
pressure at the outlet area
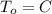 temperature at the outlet area
temperature at the outlet area
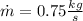 represent the flow of mass
represent the flow of mass
If we look at the first figure attached Table A-13 we see that the specific volume for the inlet condition is
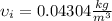 and the entropy is
and the entropy is
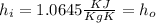
With the value of entropy and the outlet pressure of 100 Kpa we can find we specific volume at the outlet condition since w ehave the entropy
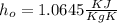
Since on the table we don't have the exact value we need to interpolate between these two values (see the second figure attached)

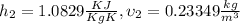
Our interest value would be given using interpolation like this:
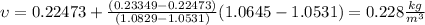
2) Solution to the problem
Now since we have all the info required to solve the problem we can find the velocities on this way.
We know from the definition of flow of mass that
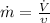 , but since
, but since
 we have this:
we have this:
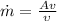
If we solve from the velocity v we have this:
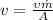 (*)
(*)
And now we just need to replace the values into equation (*)
For the inlet case:
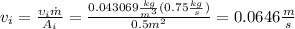
For the oulet case: