Answer:
Circle Q is 2 units to the right of circle P and 10 units above it.
Circle Q has a longer radius than circle P.
Explanation:
The equation for the circle P is
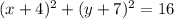
Its center is in (-4,-7) and the radius is
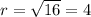
The equation for the circle Q is
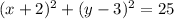
Its center is in (-2,3) and the radius is
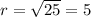
Subtracting (-2,3)-(-4,-7)=(2,10)
The center of Q is 2 units to the right of the center of P and is 10 units above.
The radius of Q is longer than the radius of P