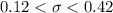Question

A commercial farm uses a machine that packages carrots in eighteen ounce portions. A sample of 7 packages of carrots has a standard deviation of 0.19. Construct the 95% confidence interval to estimate the standard deviation of the weights of the packages prepared by the machine. Round your answers to two decimal places.

Answer 1

Answer:
`0.12< \sigma<0.42`

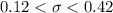
Explanation:

Confidence interval for standard deviation is given by :-

`\sqrt{(s^2(n-1))/(\chi^2_(\alpha/2))}< \sigma<\sqrt{(s^2(n-1))/(\chi^2_(1-\alpha/2))}`

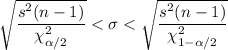
Given : Confidence level :
`1-\alpha=0.95`

⇒
`\alpha=0.05`

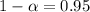
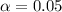
Sample size : n= 7

Degree of freedom = 6 (df= n-1)

sample standard deviation : s= 0.19

Critical values by using chi-square distribution table :

`\chi^2_(\alpha/2, df)}=\chi^2_(0.025, 6)}=14.4494\\\\\chi^2_(1-\alpha/2, df)}=\chi^2_(0.975, 6)}=1.2373`

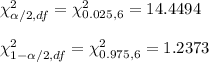
Confidence interval for standard deviation of the weights of the packages prepared by the machine is given by :-

`\sqrt{( 0.19^2(6))/(14.4494)}< \sigma<\sqrt{( 0.19^2(6))/(1.2373)}`

`\Rightarrow0.12243< \sigma<0.418400`

`\approx0.12< \sigma<0.42`

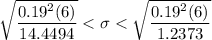
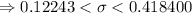
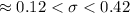
Hence, the 95% confidence interval to estimate the standard deviation of the weights of the packages prepared by the machine. :

`0.12< \sigma<0.42`