Question

A machine part has the shape of a solid uniform sphere of mass 220 g and diameter 4.50 cm . It is spinning about a frictionless axle through its center, but at one point on its equator it is scraping against metal, resulting in a friction force of 0.0200 N at that point.

Answer 1

The angular acceleration is 10.10 rad/s².

Step-by-step explanation:

Given that,

Mass of sphere =220 g

Diameter = 4.50 cm

Friction force = 0.0200 N

Suppose we need to find its angular acceleration.

We need to calculate the angular acceleration

Using formula of torque

`\tau=f* r`

`I*\alpha=f* r`

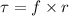
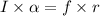
Here, I = moment of inertia of sphere

`(2)/(5)mr^2*\alpha=f* r`

`\alpha=(5* f)/(2mr)`

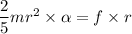
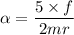
Put the value into the formula

`\alpha=(5*0.0200)/(2*220*10^(-3)*2.25*10^(-2))`

`\alpha=10.10\ rad/s^2`

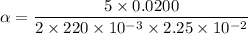
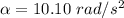
Hence, The angular acceleration is 10.10 rad/s².