Question

Consider a bicycle wheel to be a ring of radius 30 cm and mass 1.5 kg. Neglect the mass of the axle and sprocket. If a force of 20 N is applied tangentially to a sprocket of radius 4 cm for 4 seconds, what linear speed does the wheel achieve, assuming it rolls without slipping?

a) 3 m/s
b) 24 m/s
c) 5.9 m/s
d) 7.1 m/s

Answer 1

To solve the problem it is necessary to apply the Torque equations and their respective definitions.

The Torque is defined as,

`\tau = I \alpha`

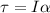
Where,

I=Inertial Moment

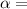`\alpha =` Angular acceleration

Also Torque with linear equation is defined as,

`\tau = F*d`

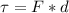
Where,

F = Force

d= distance

Our dates are given as,

R = 30 cm = 0.3m

m = 1.5 kg

F = 20 N

r = 4.0 cm = 0.04 m

t = 4.0s

Therefore matching two equation we have that,

`d*F = I\alpha`

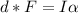
For a wheel the moment inertia is defined as,

I= mR2, replacing we have

`d*F= (mR^2a)/(R)`

`d*F= mRa`

`a = (rF)/( mR)`

`a = (0.04*20)/(1.5*0.3)`

`a=1.77 m/s^2`

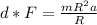
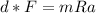
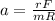
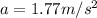
Then the velocity of the wheel is

`V = a *t \\V=1.77*4 \\V=7.11 m/s`

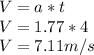
Therefore the correct answer is D.