Answer: 0.4911 kg
Step-by-step explanation:
We have the following data:
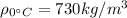 is the density of gasoline at
is the density of gasoline at
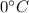
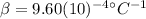 is the average coefficient of volume expansion
is the average coefficient of volume expansion
We need to find the extra kilograms of gasoline.
So, firstly we need to transform the volume of gasoline from gallons to
 :
:
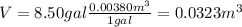 (1)
(1)
Knowing density is given by:
 , we can find the mass
, we can find the mass
 of 8.50 gallons:
of 8.50 gallons:

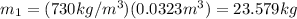 (2)
(2)
Now, we have to calculate the factor
 by which the volume of gasoline is increased with the temperature, which is given by:
by which the volume of gasoline is increased with the temperature, which is given by:
 (3)
(3)
Where
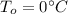 is the initial temperature and
is the initial temperature and
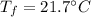 is the final temperature.
is the final temperature.
 (4)
(4)
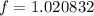 (5)
(5)
With this, we can calculate the density of gasoline at
 :
:

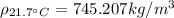 (6)
(6)
Now we can calculate the mass of gasoline at this temperature:
 (7)
(7)
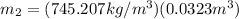 (8)
(8)
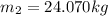 (9)
(9)
And finally calculate the mass difference
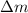 :
:
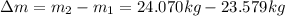 (10)
(10)
 (11) This is the extra mass of gasoline
(11) This is the extra mass of gasoline